AIDEme

An active learning-based system for interactive exploration of large datasets

Why AIDEme?

There is an increasing gap between fast growth of data and limited human ability to comprehend data. Consequently, there has been a growing demand for analytics tools that can bridge this gap and help the user retrieve high-value content from data. In this project, we develop AIDEme, a scalable interactive data exploration system for efficiently learning a user interest pattern over a large dataset. The system is cast in a principled active learning (AL) framework, which iteratively presents strategically selected records for user labeling, thereby building an increasingly-more-accurate model of the user interest. However, existing AL techniques experience slow convergence when learning the user interest on large datasets. To overcome the problem, AIDEme explores properties of the user labeling process and the class distribution of observed data to design new AL algorithms, which come with provable results on model accuracy and approximation, and have evaluation results showing much improved convergence over existing AL methods while maintaining interactive speed.

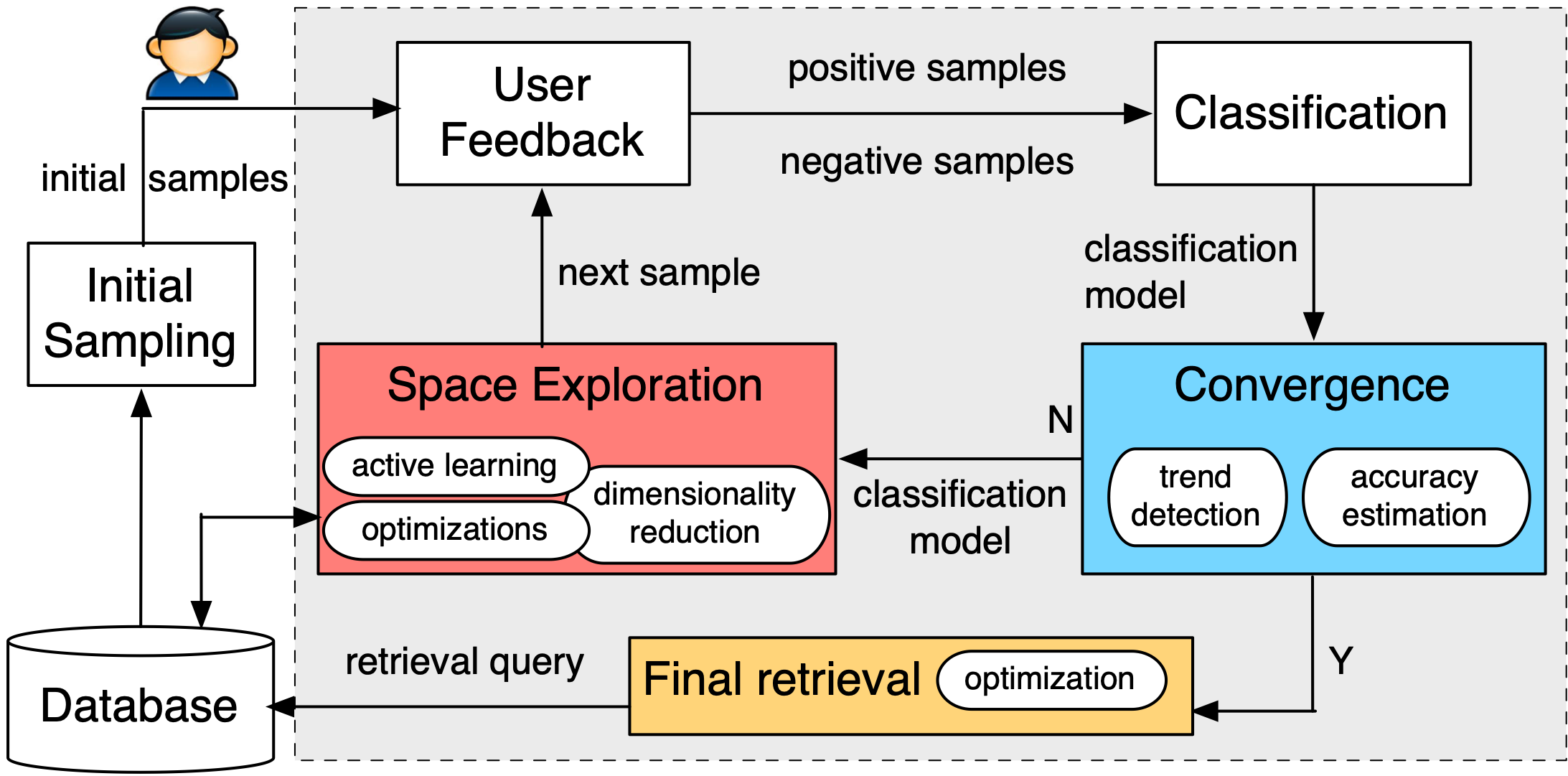
AIDEme employs a set of novel techniques to overcome the slow convergence problem:

Factorization: We observe that a user labels a data record, her decision making process often can be broken into a set of smaller questions, and the answers to these questions can be combined to derive the final answer. This insight, formally modeled as a factorization structure, allows us to design new active learning algorithms, e.g., factorized version space algorithms, that break the learning problem into subproblems in a set of subspaces and perform active learning in each subspace, thereby significantly expediting convergence.
Optimization based on class distribution: Another interesting observation is that when projecting the data space for exploration onto a subset of dimensions, the user interest pattern projected onto such a subspace often entails a convex object. When such a subspatial convex property holds, we introduce a new “dual-space model” (DSM) that builds not only a classification model from labeled examples, but also a polytope model of the data space that offers a more direct description of the areas known to be positive, areas known to be negative, and areas with unknown labels. We use both the classification model and the polytope model to predict unlabeled examples and choose the best example to label next.
Formal results on convergence: We further provide theoretical results on the convergence of our proposed techniques. Some of them can be used to detect convergence and terminate the exploration process.
Scaling to large datasets: In many applications the dataset may be too large to fit in memory. In this case, we introduce subsampling procedures and provide provable results that guarantee the performance of the model learned from the sample over the entire data source.